圆锥曲线光学性质在高考中的应用

Intro

圆锥曲线的光学性质

• 从椭圆的一个焦点发出的光线或声波，经过椭圆反射后都集中到椭圆的另一焦点上.
• 从双曲线的一个焦点射出光线，光线碰到双曲线边界反射后的路径的反向延长线经过另一个焦点.
• 从抛物线的焦点射出光线，光线碰到抛物线边界反射后的路径平行于抛物线的对称轴.

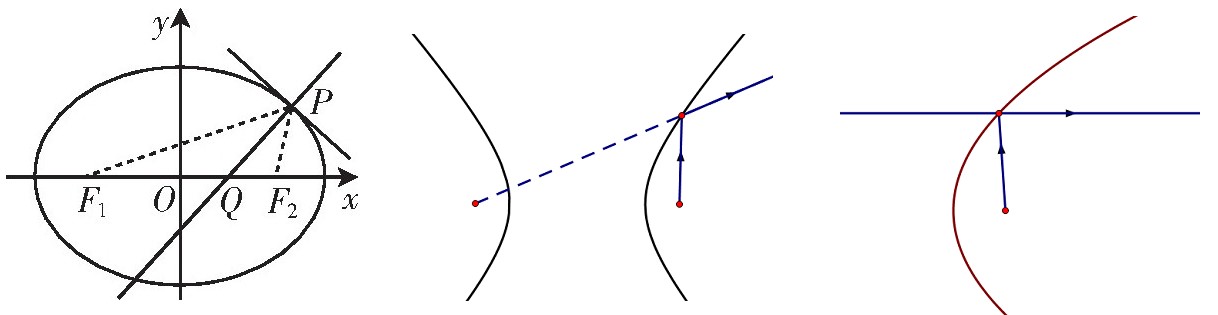
简易证明：以椭圆为例。（希尔伯特同一法）

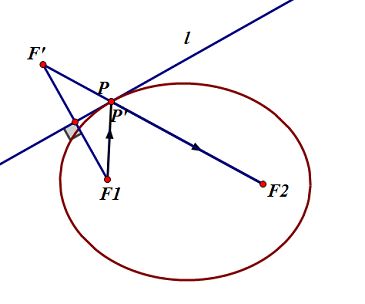
首先作出过$P \(的切线\) l \(, 然后作\) F _1 \(关于\) l \(的对称点\) F' \(, 连接\) F'F _2 \(交\) l \(于\) P'$, 如图所示.

接下来就是要说明$ P \(和\) P’$为同一点 . 首先由作图过程可知, \(P'\)为$ l $上使得 $P'F _1+ P ^′ F _2 \(最小的点 . 然后又因为\) l \(为过\) P \(的切线 , 所以有\) P ^′ F _1+ P ^′ F _2 PF _1+ PF _2$ 综上所述 , 即有$ P'F _1 ＋ P ^′ F _2 = PF _1+ PF _2 $﹐即 $P \(与\)P'$重合 . 因此 , $PF _2 $就是光线反射后的路径 .

详细证明：以椭圆为例。

如本文第一张图，则过$ P \(点的切线\) l : + =1 \(, 直线\)l\(的法线交\) x \(轴于\) Q$ , 直线$ l \(的法向量为\)=( , ) $

因$ =(-c-x_{0},-y_{0}) $, $=(c-x_{0},-y_{0}) \(, 所以\) PF_2 =$ \(c ^2+ x _0 ^{2}+y_{0}^{2}-2cx_{0}\)\(=c^{2}+x_{0}^{2}-2cx_{0}+b^{2}+ \dfrac{b^{2}x_{0}^{2}}{a^{2}}\)$ = $

同理$ |PF_{1}|^{2}= $ . 因为\(\overrightarrow n\cdot\overrightarrow{PF_{1}}\)\(= \dfrac{-cx_{0}-x_{0}^{2}}{a^{2}}- \dfrac{y_{0}^{2}}{b^{2}}\)$ = -b^{2}+ = $ $ $,

所以$ F_{1}PQ=| |= $ $ | |= . $

同理$ F_{2}PQ=| |=| |= $

所以$∠ F _1PQ = ∠ F _2 PQ $, 即过一焦点的光线经椭圆反射后必过另一焦点.

题目

1. （2013年山东高考理22(2)）椭圆$C: +y^{2}=1 \(，\)P \(是椭圆\) C \(上除长轴端点外的任一点 , 连接\) PF _1 \(与\)PF _2 \(, 设\)∠ F _1PF _2 \(的角平分线\) PM \(交\) C \(的长轴于点\) M ( m , 0 ) \(, 求\) m $的取值范围.

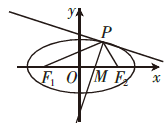
   方程$ +y^{2}=1 \(两边关于\) x \(求导得\)+2y y^{ }=0\(, 并设\)P ( x_0 , y _0 ) \(, 所以切线斜率\) k=- $,

   则$ P ( x 0 , y 0 ) \(处的法线方程\) y-y{0}= (x-x{0}) \(, 令\) y = 0 \(, 则\) m= x_{0} $, $x _0 ( -2 , 2 ) \(, 所以\) m (- , )$.

2. (2010安徽) 已知$ F _1 $, $F _2 \(为椭圆\)+ =1 \(的左右焦点 ,点\)A ( 2 , 3 ) \(在椭圆上 , 求\)∠ F _1AF _2 $的角平分线所在的直线方程.

   切线方程\(\dfrac{x_{1} x}{16}+\dfrac{y_{1} y}{12}=1\)

   \(\dfrac{2x}{16}+\dfrac{3 y}{12}=1\), 即\(\dfrac{x}{8}+\dfrac{y}{4}=1\)

   \(k=-\dfrac{1}{2}\)

   \(\therefore y-3=2(x-2)\)

   \(2x-y-1=0\)

参考资料

• 『解析几何』光学性质之美 - 知乎
• 王皓瑜.椭圆的光学性质在解题中的应用[J].中学数学,2018(11):76-77.
• 圆锥曲线光学性质秒杀高考题 - Bilibili